*PICTOGRAMAS

Un pictograma es un signo icónico dibujado y no lingüístico, que representa figurativamente (de forma más o menos realista) un objeto real, o un significado. En agrupaciones es precursor o antecedente de los sistemas de escritura propiamente dichos. Las historietas o cómics, y los chistes gráficos sin texto, son también pictogramas. Se distinguen de los ideogramas en que estos son más esquemáticos, resumidos, y abstractos; los pictogramas son más concretos.

Con su nombre se suelen denominar los signos de los sistemas no alfabéticos basados en dibujos significativos.

Un pictograma debería ser enteramente comprensible con solo tres miradas.

En el diseño de un pictograma deberían suprimirse todos los detalles superfluos.

Un pictograma es un tipo de gráfico cuya información se gráfica a través de dibujos.

Por ejemplo:

María encuestó a sus compañeros respecto a sus lugares preferidos para pasear. Con los datos, construyó el siguiente pictograma.

Con estos datos podemos decir que:

-  2 de sus compañeros prefieren el parque para pasear

- 4 de sus compañeros prefieren el cine para pasear

- 8 de sus compañeros prefieren el circo para pasear

- 6 de sus compañeros prefieren el museo para pasear

Además podemos decir que en el curso de maría hay un total de 26 alumnos.

-  6 de sus compañeros prefieren el zoológico para pasear

*POLÍGONOS DE FRECUENCIA

Polígono de frecuencia es el nombre que recibe una clase de gráfico que se crea a partir de un histograma de frecuencia. Estos histogramas emplean columnas verticales para reflejar frecuencias): el polígono de frecuencia es realizado uniendo los puntos de mayor altura de estas columnas.

Es decir, por tanto, podríamos establecer que un polígono de frecuencia es aquel que se forma a partir de la unión de los distintos puntos medios de las cimas de las columnas que configuran lo que es un histograma de frecuencia. Este se caracteriza porque utiliza siempre lo que son columnas de tipo vertical y porque nunca debe haber espacios entre lo que son unas y otras.

En las ciencias sociales, en las ciencias naturales y también en las económicas es donde con más frecuencia se hace uso de estos mencionados histogramas ya que se emplean para llevar a cabo lo que es la comparación de los resultados de un proceso determinado.

  

*HISTOGRAMAS

En estadística, un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o de la muestra, respecto a una característica, cuantitativa y continua (como la longitud o el peso).


 De esta manera ofrece una visión de grupo permitiendo observar una preferencia, o tendencia, por parte de la muestra o población por ubicarse hacia una determinada región de valores dentro del espectro de valores posibles (sean infinitos o no) que pueda adquirir la característica.


Así pues, podemos evidenciar comportamientos, observar el grado de homogeneidad, acuerdo o concisión entre los valores de todas las partes que componen la población o la muestra, o, en contraposición, poder observar el grado de variabilidad, y por ende, la dispersión de todos los valores que toman las partes, también es posible no evidenciar ninguna tendencia y obtener que cada miembro de la población toma por su lado y adquiere un valor de la característica aleatoria mente sin mostrar ninguna preferencia o tendencia, entre otras cosas.

Se utilizan para relacionar variables cuantitativas continuas. Para variables cuantitativas discretas las barras se dibujan separadas y el gráfico se llama diagrama de frecuencias, porque la variable representada en el eje horizontal ya no representa un espectro continuo de valores, sino valores cuantitativos específicos, igual que ocurre en un diagrama de barras, usado para representar una característica cualitativa o categórica. Su utilidad se hace más evidente cuando se cuenta con un gran número de datos cuantitativos y que se han agrupado en intervalos de clase.
Ejemplos de su uso es la representación de edades o estaturas de una población. Por comodidad, sus valores se agrupan en clases, es decir, en intervalos continuos. En los casos en los que los datos son cualitativos (no numéricos), como sexto grado de acuerdo o nivel de estudios, espreferible un diagrama de sectores.

*PASTEL

El diagrama circular (también llamado gráfica circular, gráfica de pastel o diagrama de sectores) sirve para representar variables cualitativas o discretas. Se utiliza para representar la proporción de elementos de cada uno de los valores de la variable.

Consiste en partir el círculo en porciones proporcionales a la frecuencia relativa. Entiéndase como porción la parte del círculo que representa a cada valor que toma la variable.

Cálculo de los sectores

Un círculo completo son 360º (o 2π radianes). El ángulo de cada porción debe ser proporcional a la frecuencia de cada valor. Por ejemplo, si un valor representa un 50% del total de elementos, su sector del círculo tendrá un ángulo de 180º (o π radianes).

Sea (X₁,X₂,…,X_N) un conjunto de elementos. La fórmula para calcular el ángulo de cada sector es la siguiente:

El ángulo de cada sector se calcula como 360º dividido por el total de sujetos (N) y multiplicado por la frecuencia absoluta (n_i), o bien el producto de la frecuencia relativa (f_i) por 360º. También podemos calcular el ángulo en radianes:

Ejemplo

Los continentes suponen el 29,1% de superficie de la Tierra, el resto es agua. Supongamos que se pretende representar mediante un diagrama circular la proporción de superficie de cada continente respecto a la superficie de todos los continentes.

Para dibujar el diagrama, calcula el ángulo de cada uno de los sectores (que serán Europa, África, América, Asia, Oceanía, la Antártida). Se obtiene la siguiente tabla:

Una vez calculados los ángulos, puede representarlos gráficamente. El diagrama circular será el siguiente:

*DIAGRAMA DE BARRAS 

Para realizar esta representación tomamos el primer cuadrante de un sistema de coordenadas donde el eje de abscisas se corresponderá con las modalidades y el de ordenada con las frecuencias, éstas pueden ser absolutas o relativas. 
Veamos con un ejemplo como queda.

En una empresa se desea conocer el color de ojos de sus empleados, se observa a los 50 empleados y se obtienen los siguientes resultados: 

Color ojos Empleados Negros 14 Marrones 24 Verdes 4 Azules 8

El diagrama de barras asociado es:

En otras ocasiones tenemos los datos de dos variables y queremos representarlos en un mismo diagrama de barras para compararlos, lo más probable es que no haya el mismo número de observaciones en cada una de ellas, por lo que no sería acertado representar el diagrama de barras con las frecuencias absolutas, en este caso las frecuencias relativas son más adecuadas para su representación.
Dos  empresas estudian el estado civil de sus empleados con el siguiente resultado:

Diagrama de barras para variables cuantitativas discretas
El procedimiento a seguir es similar al del caso cualitativo, con la salvedad de que ahora podremos obtener también diagramas de barras acumulados, cosa que no era posible determinar en el caso cualitativo.

Consideremos el número de habitantes por vivienda en Andalucia en 2001,según el Instituto Andaluz de Estadística.
La variable número de habitantes es cuantitativa por tanto podemos ordenar sus modalidades y realizar un estudio acumulado.

*LLANO

El ángulo llano es, en términos de la geometría, el espacio comprendido en una intersección entre dos rectas cuya apertura mide 180 grados o 180º. Como el ángulo es de 180º no hay una diferencia entre dos rectas o una recta y podemos decir que los ángulos en una línea recta siempre suman 180º.

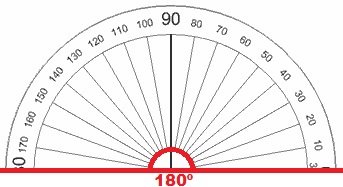La característica principal de los ángulos llanos es que cuando cambia de dirección ésta será siempre la contraria. Podemos asociarlo a la expresión popular ‘giro de 180 grados’ cuando una persona cambia completamente su opinión para la dirección contraria por ejemplo: "La semana pasada defendía los derechos de los inmigrantes y ahora quiere crear una ley para echarlos del país, ¡dio un giro de 180º en su discurso!".

Si tomamos un círculo, los cuales miden 360º, podemos decir que la mitad del círculo son 180º o sea un ángulo llano. Y la mitad de un ángulo llano son 90º o sea un ángulo recto.

Se puede medir los ángulos con un transportador. Los transportadores más comunes son precisamente de 180º o sea completan un ángulo llano.

Se cree que el origen de los 360º para un círculo completo provenga de los calendarios antiguos, como el de los persas y el de los egipcios, que ya tenían 360 días por año. Los antiguos observaron en las estrellas que giran alrededor de la estrella polar, que éstas se mueven un grado por día hasta trazar un círculo completo en 360 días.

*CÓNCAVO

En ángulo es una figura de la geometría que se forma por dos semirrectas que comparten el mismo vértice como origen. El adjetivo cóncavo, que proviene del vocablo latino concluso, alude por su parte a aquello que exhibe una curva hacia dentro.

La idea de ángulo cóncavo suele entenderse con relación a la noción de ángulo convexo. Para esto debemos considerar que, en un mismo plano, dos semirrectas que no se encuentran alineadas ni son coincidentes y que comparten origen, siempre dan lugar a dos ángulos: un ángulo cóncavo y un ángulo convexo. El ángulo cóncavo es el más amplio, mientras que el ángulo convexo es el que tiene la amplitud menor.

Para evaluar la dirección de la curva que exhiben estos ángulos, es necesario un punto de vista: cuando decimos «hacia dentro», hacemos referencia a una curva que se aleja del observador y «se adentra» en el círculo imaginario que completan el ángulo convexo y el cóncavo. Del mismo modo, el ángulo convexo tiene su punto central más prominente que el resto, es decir que se encuentra más cerca del observador y sobresale de dicho círculo.Los ángulos cóncavos, también llamados ángulos entrantes o ángulos reflejos, miden más de 180° pero menos de 360°. 

*OBTUSO

El ángulo obtuso es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o abertura es mayor que 90 grados (90°) y menor que 180 grados (180°).

Los ángulos obtusos se pueden encontrar, por ejemplo, en los triángulos obtusángulos ya que se caracterizan precisamente por tener uno de sus ángulos obtuso, o sea, mayor a 90 grados y menor a 180 grados.

En geometría, es importante saber identificar los ángulos obtusos, ya que, al ser visualmente mayor de 90° (un cuarto de un círculo), se hace visualmente más fácil determinar, por ejemplo, que sus ángulos suplementarios (ángulos que sumados dan 180 grados) deben ser agudos (menores de 90 grados) y otras operaciones básicas en trigonometría.

En la clasificación de triángulos, podemos encontrar el ángulo obtuso en un triángulo obtusángulo escaleno. Este tipo de triángulo se caracteriza por poseer un ángulo obtuso y todos sus lados desiguales. Esta última característica es común a todos los triángulos escalenos

                                   .

*AGUDO

Lo primero que vamos a hacer antes de entrar de lleno en el establecimiento del significado del término ángulo agudo es conocer el origen etimológico de las dos palabras que le dan forma:
-Ángulo, en primer lugar, deriva del griego. En concreto, emana de “anuloso”, que puede traducirse como “doblado” y que luego pasó al latín como “angulus”, donde ya toma el significado de “ángulo”.
-Agudo, por otro lado, tiene su origen en latín, exactamente en la palabra “acutus”, que es sinónimo de “agudo”. Esa a su vez procede del verbo “acuere”, que es sinónimo de “afilar”.

Dos semirrectas que comparten un mismo vértice como punto de origen forman un ángulo. De acuerdo a las características que se analicen, es posible diferenciar entre múltiples tipos de ángulos.

Un ángulo agudo es un ángulo que mide más de 0º y menos de 90º. Esto quiere decir que, si solo consideramos los números enteros, un ángulo agudo mide entre 1º y 89o. Esta definición sobre las medidas de los ángulos agudos nos permite afirmar que se trata de ángulos mayores que los ángulos nulos (cuya medida es igual a 0º) pero menores que los ángulos rectos (90º), los ángulos obtusos (más de 90º y menos de 180º), los ángulos llanos (180º) y los ángulos perigonales (360º).

                                             

*RECTO

El ángulo recto es el espacio entre dos rectas que comparten el mismo vértice y cuya apertura es de 90 grados (90º).

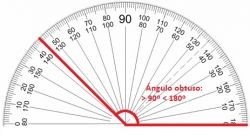
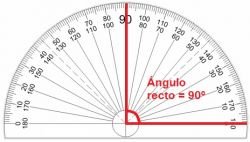En geometría, el ángulo recto es importante, ya que, es fácil determinar cuando se encuentran dos rectas perpendiculares, por ejemplo:

• 
  
• En la geometría analítica se obtienen planos cartesianos,
• En trigonometría, se puede determinar de manera más rápida e intuitiva los ángulos que componen un triángulo. En un triángulo rectángulo, podemos distinguir fácilmente el ángulo recto y, por ende, concluir que los otros dos ángulos son agudos o menores de 90º.

Además, los ángulos rectos o ángulos de 90 grados es la referencia entre los de menor (ángulos agudos) y de mayor grado (ángulos obtusos) lo que, una vez más, ayuda a visualizar y determinar los tipos de ángulos de las figuras geométricas estudiadas.

                                                   

*RANGO DE VARIACIONES

Rango es una categoría que puede aplicarse a una persona en función de su situación profesional o de su estatus social. Por ejemplo: “Tenemos que respetar el rango del superior a la hora de realizar algún pedido”, “Diríjase a mi sin olvidar su rango o será sancionado”

El concepto también puede hacer referencia al nivel o la categoría de algo: “El hotel está fuera de nuestro rango de presupuesto”, “Teniendo en cuenta los resultados, podemos aspirar a estar en el rango que va del quinto al décimo puesto”.

De la misma forma tenemos que subrayar que en Ecuador se hace uso del término rango con otra acepción. Concreta mente nos encontramos con el hecho de que en este país el citado concepto se utiliza para definir a una fila de escolares que se hallan perfectamente alineados.

Se conoce como rango militar sistema jerárquico que establece la escalada de mando dentro de las fuerzas armadas. Este rango es visible a partir de la utilización de insignias en el uniforme, por lo general adheridas al pecho o a los hombros del militar.

En el caso del ámbito militar tenemos que dejar patente que los rangos están perfectamente claros y delimitados. Así, concreta mente existen cuatro grandes grupos dentro de los cuales a su vez también se establecen sus propios rangos:

Oficiales Generales. Dentro de esta clasificación están el Capitán General, el General, el Teniente General, el General de División y el General de Brigada.

Oficiales. En su caso, este grupo se conforma a su vez por diversos rangos: Coronel, Teniente Coronel, Comandante, Capitán, Teniente, Alférez…

Suboficiales. Los rangos que se establecen dentro de esta denominación son: Suboficial mayor, Subteniente, Brigada, Sargento primero y Sargento.

Tropa. En este cuarto grupo militar los rangos establecidos son los siguientes: Cabo Mayor, Cabo Primero, Cabo, Soldado de Primera y Soldado.

En el campo de la estadística, el rango señala la amplitud de la variación de un fenómeno entre su límite menor y uno claramente mayor. El rango estadístico, por lo tanto, es el intervalo que contiene dichos datos y que puede calcularse a partir de restar el valor mínimo al valor máximo considerado.

En álgebra, el rango de una matriz es el número de columnas que son independientes desde el punto de vista lineal.

*PROMEDIO

El concepto de promedio se vincula a la media aritmética, que consiste en el resultado que se obtiene al generar una división con la sumatoria de diversas cantidades por el dígito que las represente en total. Claro que esta noción también se utiliza para nombrar al punto en que algo puede ser dividido por la mitad o casi por el medio y para referirse al término medio de una cosa o situación.

El resultado que arroja el cálculo del promedio, por supuesto, no siempre coincide con la realidad: por eso se habla de una media. Supongamos que, en barrio con cien casas, viven doscientos perros. El promedio indica que habitan dos perros por casa. En la realidad, sin embargo, algunas casas cuentan con tres o más perros, mientras que en otras no vive ningún can.El segundo concepto que se utiliza cuando se está operando con números y datos en este sentido es el de moda. Esta se emplea para referirse al dato que se repite con más frecuencia entre todos aquellos.

Esto demuestra que un promedio es sensible a los valores extremos. Los valores muy elevados tienden a aumentar el promedio, mientras que los valores muy bajos lo reducen. De este modo, el promedio puede dejar de ser representativo por alejarse de la media de la población.